Binary Relations

A binary relation is a mathematical object that maps elements from one set, called the domain, to another set, called the codomain.

Now, let's look at the definition of a function:

Functions are mappings that assign elements from one set (domain) to another (codomain).

The distinction is that in a function, every element should only map to at most one element, so, for example, an element $a$ in domain $A$ can only be mapped to $b$ in codomain $B$, not both $b$, and $c$, etc.

So, a function is a special case of a binary relation.

A function that maps elements in domain $A$ to elements in codomain $B$ is denoted as $f : A \rightarrow B$.

If a function is a partial function, some elements in the domain can be undefined (some elements in the domain don't have an arrow coming out). For example, $f(x) = \frac{1}{x^2}$ does not assign a value to $0$.
On the other hand, if every element in the domain is defined, it is called a total function.

Function composition is as simple as taking the value of one function, and passing it to another one:

A binary relation $R$ has a set $A$, domain of $R$; a set $B$, codomain of $R$; and a subset of $A \times B$, the graph of $R$ (this is the relation part — arrows from $A$ to $B$).

The notation is similar to functions: $R : A \rightarrow B$. This is a relation "between $A$ and $B$" (or, "from $A$ to $B$").
If the domain and codomain are the same set $A$, we can say that the relation is "on $A$".

When a pair $(a, \ b)$ is in the graph of $R$, it is denoted as $a \ R \ b$.

The image of a set $X$, under a relation $R$, is written as $R(X)$. It is the codomain set.

For example, look at this diagram:

$X$ is the domain, $Y$ is the codomain, graph of $R$ is $\{(1, D), \ (2, C), \ (3, C)\}$

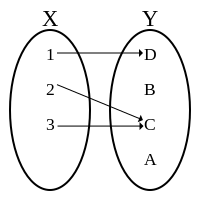
Range is the actual elements with arrows coming in. In this example, while $Y$ is the codomain, $\{D, \ C\}$ is the range.
So, the range is not always equal to codomain — it can be equal to, or smaller than the codomain.

The set of points with an arrow coming in from $X$ is the $R(X)$, the image of $X$.

We can write it in logical notation as such:

$Y$ is the codomain set, and $b$ is an element in it; $X$ is the domain set, and $a$ is an element in it.

So, the formula above says that $R(X)$ is the set of $b$ in $Y$ such that there exists an $a$ in $X$ such that $(a, \ b)$ is a pair that's in the graph of $R$ (remember that's what $a R b$ means).

This part itself $[\exists a \in X \ a R b]$ indicates that there is an arrow to $b$ coming from the set of $X$.

The inverse of a relation $R : A \rightarrow B$ is denoted as $R^{-1}$, and it is the relation from $B$ to $A$. It just flips the arrows around, so the codomain becomes the domain, and the domain becomes the codomain.
$R^{-1}(x)$ called the inverse image of $x$ under $R$.

This formula holds true: $aRb \iff bR^{-1}a$
An arrow coming from $a$ ends in $b$, and vice versa, an arrow that ends in $b$ is coming from $a$.

Now, there are some terms that we are going to take a look at:

• total relation: there is at least one arrow out of every domain element. (in a relation from $A$ to $B$, every element in set $A$ has to have an arrow going out)

  • $R$ is total iff $A = R^{-1}(B)$.
  • If a relation is both total and a function, that means there is exactly one arrow coming out of every domain element.

• surjective relation: there is at least one arrow into every codomain element (the range is the entire codomain).

  • $R$ is surjective iff $R(A) = B$
  • $|A| \geq |B| \ (\text{for finite } A, \ B)$
  • Example of a non-injective surjective function:
    

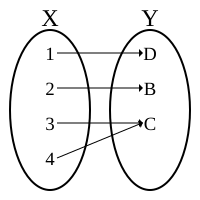
• injective relation: there is at most one arrow into every codomain element.

  • $|A| \leq |B| \ (\text{for finite } A, \ B)$
  • Example of an injective non-surjective function:
    

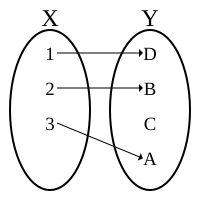
• bijective relation: there is exactly one arrow out in every domain element, and exactly one arrow in every codomain element (one-to-one correspondence).

  • $|A| = |B| \ (\text{for finite } A, \ B)$
  • Example of a bijection (injective surjective function):
    

Here is a nice way to keep these in mind: think of totality, surjection, function, and injection as superheroes who are responsible for inspecting the arrows from one set to another.

Totality is concerned with the domain, surjection is concerned with the codomain. Both of them want at least one arrow.

Function is concerned with the domain, injection is concerned with the codomain. Both of them want at most one arrow.

Bijection always wants one-to-one correspondence.

$R$ is a function iff $R^{-1}$ is an injection.
$R$ is a surjection iff $R^{-1}$ is total.
$R$ is an injection iff $R^{-1}$ is a function.
$R$ is a bijection iff $R^{-1}$ is a bijection.

• previous
• next