Logic & Propositions

In place of specific propositions, usually the letters $P$ or $Q$ are used to indicate that these can only take on the values T (true) or F (false).

Connectives:

These are the connectives that are mostly used:

• Negation just inverses the truth value of a proposition.

• A conjunction is true only if both propositions are true.

• A disjunction is true if one of the propositions is true.

• An exclusive disjunction, "exclusive or (XOR)," is true when the both of the propositions are of different truth values.

• A biconditional is true when both of the propositions are of the same value.

• An implication is only false when the antecedent (the "if part") is true, and the consequent (the "then part") is false; in all other cases it is true. In fact, let's take a look at one example:
  The statement is: "If Goldbach's conjecture is true, then $x^2 \geq 0$ for every real number $x$."

  Remember that Goldbach's conjecture says that every even integer greater than 2 is the sum of two primes.

  We don't know for certain if it is true or not, but "$x^2 \geq 0$ for every real number $x$" is definitely true. So, it doesn't matter if the antecedent (If Goldbach's conjecture is true) is true or not, the fact that the consequent (then $x^2 \geq 0$ for every real number $x$) is true makes the whole proposition true.

From an implication ($p \implies q$), we can construct 3 new conditional statements:

• converse ($q \implies p$) — switching $p$ and $q$
• inverse ($\neg p \implies \neg q$) — negate both $p$ and $q$
• contrapositive ($\neg q \implies \neg p$) — switch & negate both $p$ and $q$

An implication and its contrapositive are equivalent:

An implication and its converse is the same as the biconditional:

A tautology is a proposition that is always true (e.g., $p \lor \neg p$)

A contradiction is a proposition that is always false (e.g., $p \land \neg p$)

A contingency is a proposition that is neither a tautology nor a contradiction (e.g., $p$)

Equivalence

Assignment of values to variables is called an environment.
For example, environment $v$ assigning truth values to $P$, $Q$, and $R$: $v(P) = T, \ v(Q) = T, \ v(R) = F$.
Two propositional formulas are equivalent iff they have the same truth value in all environments. That is, the compound propositions $p$ and $q$ are logically equivalent if $p \implies q$ is a tautology. Equivalency is denoted as $p \equiv q$ (e.g., $\neg p \lor q \equiv p \implies q$).

An example is De Morgan's Laws:

A half adder is a digital circuit that adds two 1-bit numbers. A full adder also adds two 1-bit numbers, but the difference is that a half adder does not have a carry input while a full adder does. (Carry is the same thing when you do decimal addition, for example, with $21 + 9$, you first add $9$ and $1$, the result is $10$, so you carry the $1$ to add it to $2$.)

1-bit half adder	1-bit full adder

A binary addition circuit example (a "ripple carry") is as follows:

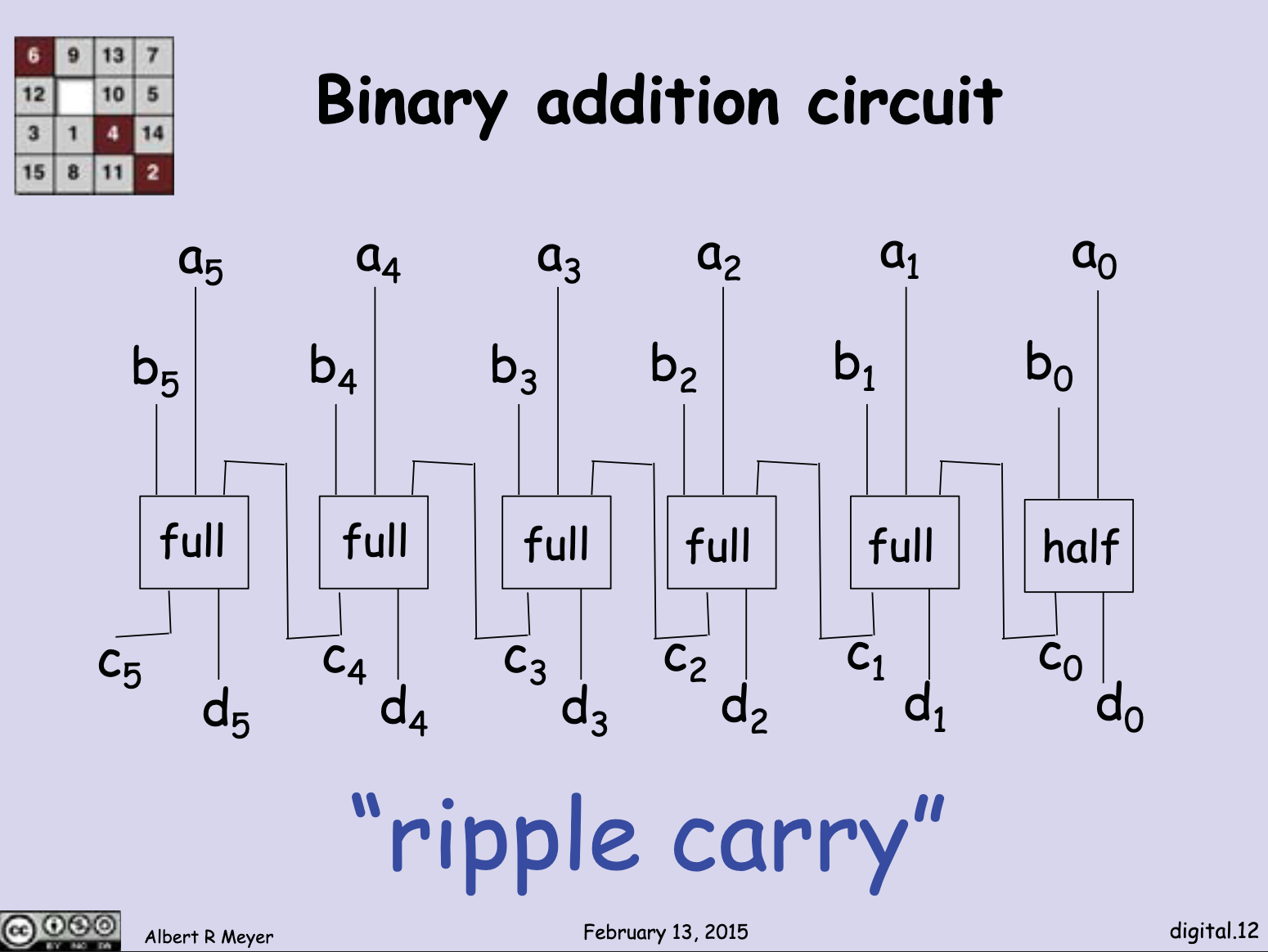
We can say that $d_0$ is $a_0 \oplus b_0$, and $c_0$ is $a_0 \land b_0$.
(Imagine $a_0$ as $1$, and $b_0$ as $1$, adding them will result in $2$ which is $10$ in binary — so, you write $0$ and carry the $1$, and the operations hold. The bit you write is the xor of two bits, and the carry is the and of them).

If we define $s_i$ to be $a_i \oplus b_i$, and $d_i$ to be $c_{i - 1} \oplus s_i$, $c_i$ is going to be $(c_{i - 1} \land s_i) \lor (a_i \land b_i)$.

What does it mean? Let's see.

Satisfiability & Validity

A formula is satisfiable iff it is true in some environment (which can sometimes be true), for example, $P$.

An example of a formula that is not satisfiable is $P \land \neg P$.

A formula is valid iff it is true in all environments (which is always true), for example, $P \lor (\neg P)$ (also called a tautology).

• previous
• next