Coloring & Connectivity

The graph coloring problem requires that we color the adjacent vertices with different colors, and use as few different colors as possible.

An example graph with $3$-coloring:

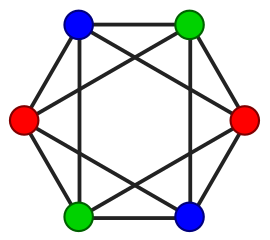
A graph $G$ is said to be $k\text{-colorable}$ if it has a coloring that uses at most $k$ colors.
The minimum value of $k$ is the graph's chromatic number, denoted as $\chi(G)$.

It is a challenging problem, to say the least.

The chromatic number of a cycle that has even-numbered vertices is $2$: $\chi(C_{\text{even}}) = 2$.
An odd-length cycle requires $3$ colors: $\chi(C_{\text{odd}}) = 3$.

A complete graph $K_n$ will require $n$ colors because all the vertices are adjacent to each other: $\chi(K_n) = n$.

A bipartite graph $G$ has a chromatic number of $2$: $\chi(G) = 2$.

A graph $G$ is $k$-colorable iff $\chi(G) \leq k$.

A graph with maximum degree at most $k$ is $(k + 1)\text{-colorable}$.

The maximum degree is the largest vertex degree in a graph. In our example, it is 4. So, our graph is 5-colorable.

That is, if every vertex has at most $k$ degrees, then $\chi(G) \leq k + 1$.

A graph is connected when every pair of its vertices are connected.

A subgraph is exactly what you might think it is; $G$ is a subgraph of $H$ iff $V(G) \subseteq V(H)$ and $E(G) \subseteq E(H)$.

A connected component of a graph is a subgraph that has some vertex and everything that is connected to it.

So, $\text{the connected component of vertex } v = \{w \ | \ v \text{ and } w \text{ are connected.}\}$

The connection strength is measured by the number of links that fail before connectedness fails.

What does it mean?

Vertices $v$ and $w$ are $k\text{-edge connected}$ if they remain connected whenever fewer than $k$ edges are removed. That is, when it takes at least $k$ failures to disconnect them, two vertices are $k\text{-edge connected}$.

In other words, $k - 1$ is the amount of edges you can remove without breaking the connectivity between two vertices.
You can remove any amount of edges up to $k$, and the vertices will stay connected.

Need more definitions? Here is another one:

Two vertices are $k\text{-edge connected}$ when it takes at least $k$ “edge-failures” to disconnect them.

For example, a complete graph, $K_n$, is $(n - 1)\text{-connected}$.
Every cycle is $2\text{-connected}$.

If two vertices are connected in a graph $G$, but not connected when an edge $e$ is removed, then $e$ is called a cut edge of $G$.

• previous
• next