Degrees & Isomorphism

In a graph, when two different vertices are connected by only one edge, and that edge is undirected, we have a simple graph. Simple as that.
We can represent an edge connecting $u$ and $v$ as: $\textlangle{u — v} \textrangle$

The vertices of an undirected edge are called the endpoints of that edge.
So, where $u \neq v$, the endpoints of $\textlangle{u — v} \textrangle$ are $u$ and $v$.

Here is an example of a simple graph:

If we call this graph $H$, then the vertices can be represented as:

$V(H) = \{A, \ B, \ C, \ D, \ E, \ F\}$

And, the edges are:

$E(H) = \{\textlangle{A — B} \textrangle, \ \textlangle{A — C} \textrangle, \ \textlangle{B — D} \textrangle, \ \textlangle{C — D} \textrangle, \ \textlangle{C — E} \textrangle, \ \textlangle{E — F} \textrangle \}$

Note that using capital letters for vertices is probably not a good idea.

Two vertices are adjacent if they are the endpoints of the same edge.
For example, $A$ and $B$ are adjacent.
An edge is incident to its endpoints.
For example, the edge $\textlangle{A — B} \textrangle$ is incident to $A$ and $B$.
The number of edges incident to a vertex is called that vertex's degree.
For example, the degree of the vertex $A$ is $2$.

Simple graphs don't have self-loops.
As opposed to simple graphs, multigraphs have two endpoints that have more than one edge connecting them.

According to the handshaking lemma:

The sum of the degrees of vertices in a simple graph equals twice the number of edges.

It's because every edge contributes two to the sum of the degrees, one for each of its endpoints.

It also implies that the sum of the degrees can't be odd, because it's twice the number of edges:

A complete graph $K_n$ is a simple graph that has exactly one edge between each pair of $n$ distinct vertices.

An example:

On the other hand, an empty graph has no edges.

An example:

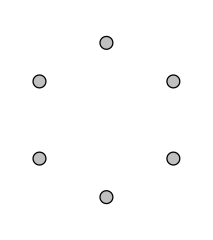
Note: For more special types of graphs, Kimberly Brehm's video does a pretty good overview.

We mentioned the concept of isomorphism briefly in Partial Orders and Equivalence, but let's take a look at it once more.

An isomorphism between graphs $G$ and $H$ is a bijection $f \ : \ V(G) \rightarrow V(H)$ such that $\textlangle{u — v} \textrangle \in E(G) \ \text{ iff } \ \textlangle{f(u) — f(v)} \textrangle \in E(H)$ for all $u$, $v$ in $V(G)$.

So, two graphs should have the same connections.

An example:

$G$	$H$

A simple graph is a bipartite graph if its vertices can be partitioned into two sets, $L(G)$ and $R(G)$ such that every edge has one endpoint in $L(G)$ and the other endpoint in $R(G)$:

• previous
• next