Directed Acyclic Graphs

A directed graph with no cycles is called a directed acyclic graph.

By definition, they also don't have closed walks (remember that a closed walk is a walk that begins and ends at the same vertex).

Also called DAGs, directed acyclic graphs are helpful for things such as task scheduling:

A schedule for performing tasks specifies which tasks to do at successive steps.

In a scheduling problem, some tasks depend on other tasks being completed beforehand. Because of that, we need to order the tasks. Such ordering is called topological sorting:

A topological sort of a finite DAG is a list of all the vertices such that each vertex $v$ appears earlier in the list than every other vertex reachable from $v$.

There is a possibility that there is no minimum vertex in a DAG, but there can be a lot of minimal ones.

Two vertices are said to be comparable if one of them is reachable from the other.

In a set of vertices, when any two of them are comparable, it is called a chain. It implies that the sequence of elements has an order.

The opposite of that, when no two elements are comparable, is the antichain.

So, $u$ is incomparable to $v$ iff there is no path from $u$ to $v$ and no path from $v$ to $u$.

When a vertex in a chain is reachable from all the other vertices, it is the maximum element of the chain.

Every $n$-vertex DAG has a chain of size greater than $\sqrt{n}$, or an antichain of size greater than or equal to $\sqrt{n}$. If we have a DAG with $n$ number of vertices, for any number $t \gt 0$, it either has a chain of size bigger than $t$, or it has an antichain of size greater than or equal to $\frac{n}{t}$ for all $1 \leq t \leq n$.

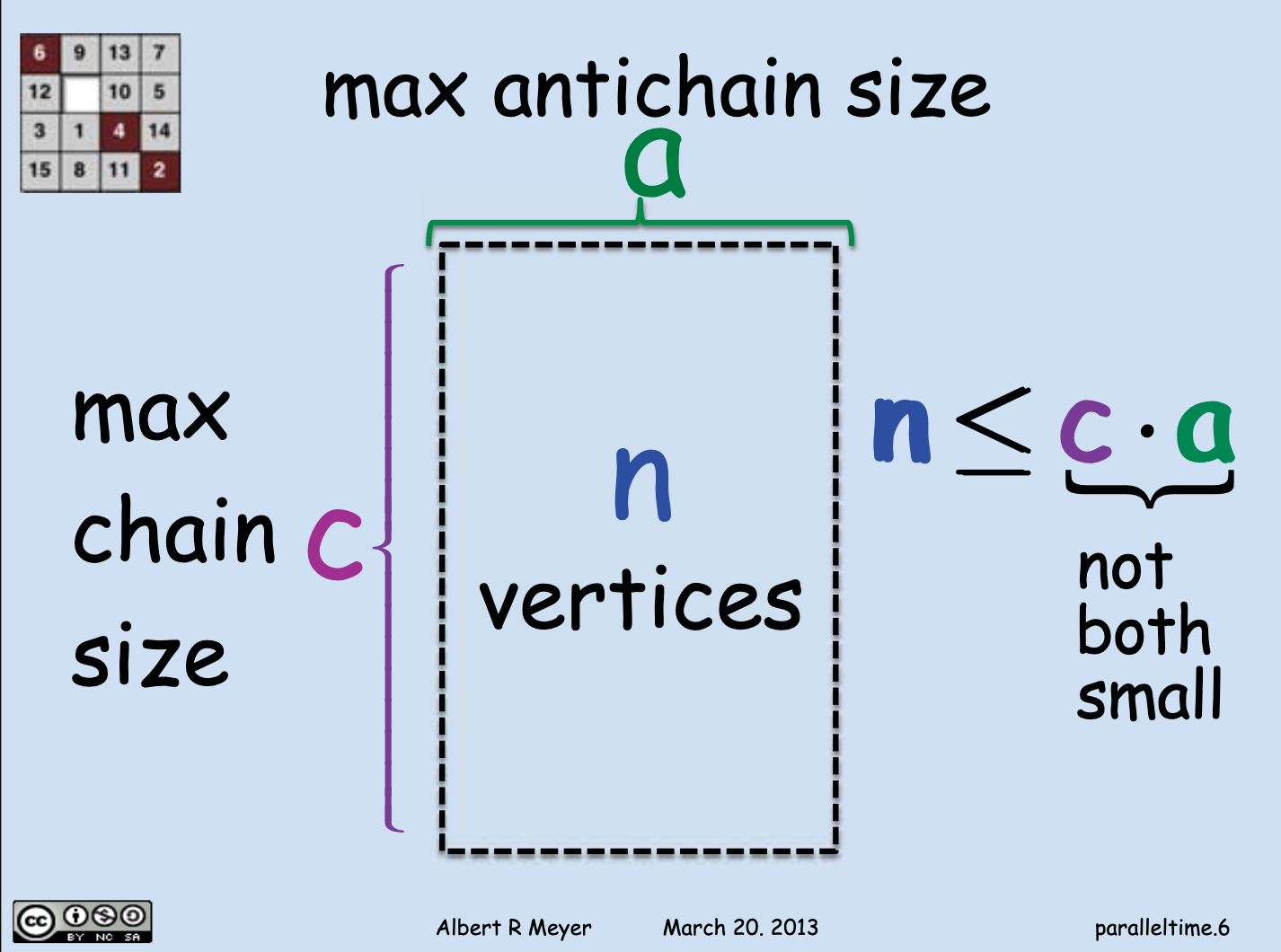
The product of the maximum chain size and the maximum antichain size is greater than or equal to the number of vertices:

This is Dilworth's lemma.

To help visualize it better in our mind's eye, it'd be good to know that the size of the longest chain is called the length, and the size of the longest antichain the width.

Then, this image taken from the slides of the lecture would make more sense:

A partition of a set $A$ is a set of nonempty subsets of $A$ such that every element of $A$ is in exactly one of them. These nonempty subsets are called blocks of the partition.

So, every element of $A$ has to be in exactly one block.

Let's imagine a set $\{a, \ b, \ c, \ d, \ e\}$.
We can think of a partition of it into three blocks, such as: $\{\{a, \ c\}, \ \{b, \ e\}, \ \{d\}\}$.

A parallel schedule for a DAG is a partition of its vertices into blocks $A_0, \ A_1, \ ...,$ such that when $j \lt k$, no vertex in $A_j$ is reachable from any vertex in $A_k$.
So, for example, the vertices in $A_0$ can't be reachable from any vertex in $A_1$.

The block $A_k$ is the set of elements scheduled at step $k$.
The number of blocks is the time of the schedule.

The largest chain ending at element $a$ is the critical path to $a$.
The number of elements in the chain that are less than $a$ is the depth of $a$.
So, in a parallel schedule, before task $a$ can even be started, there must be at least depth(a) steps.

• previous
• next