Trees

Let's talk about simple graphs without cycles.

A forest is an acyclic graph.
A tree is a connected acyclic graph.

Nodes with degrees of $1$ are called the leaves.

Here is one example:

Note: This section assumes some familiarity with terminology like the root node, parent node, child node, etc.

Let's look at some properties of trees:

• Every connected subgraph is a tree.
  (If a subgraph has a cycle, then the whole graph has that cycle. Likewise, if a graph is acyclic, that means the subgraphs are also acyclic. Then, if a subgraph is connected, it is a tree.)

• There is a unique path between every pair of vertices.
  (A tree is connected, which means that every vertex pair has at least one path.
  But, suppose that there are two different paths ($p \neq q$) between two vertices. That means the minimum total length is $|p| + |q|$. If these paths have a common vertex $w$ (not the starting or the ending one), then there are distinct paths between our vertices with a length less than $|p| + |q|$, that is, one possible path has the length (a part of the path $p$) + (a part of the path $q$). But that would contradict our starting assumption that the minimum total length must be length of $p$ + length of $q$. Therefore, $p$ and $q$ can't have other vertices in common besides their endpoints.)

• Adding an edge between nonadjacent nodes in a tree creates a graph with a cycle.
  (Since there is already a unique path between two vertices $u$ and $v$, when you add another edge $\textlangle{u — v} \textrangle$, well, that forms a cycle.)

• Removing any edge disconnects the graph (every edge is a cut edge).
  Likewise, that implies that if an edge is on a cycle, that is not a cut edge.
  (Two vertices have a unique path, and if we remove the edge connecting them, what's there to connect them anymore? It was all that they had, so if we remove that edge, there will be no path left connecting them.)

• If the tree has at least two vertices, then it has at least two leaves.

• The number of vertices in a tree is one larger than the number of edges. (If a tree has $n$ number of vertices, it has ($n - 1$) number of edges.)

Chromatic number of a tree with more than or equal to 2 vertices is 2: $\chi(\text{tree}) = 2$

We can choose any vertex as a root node and color the even-length distance vertices a certain color and the odd-length vertices another color, alternating between levels.

A subgraph that is a tree with all the vertices of the whole graph is called a spanning tree.
So, it is a subgraph that has all the vertices of the whole graph.

Here is one example:

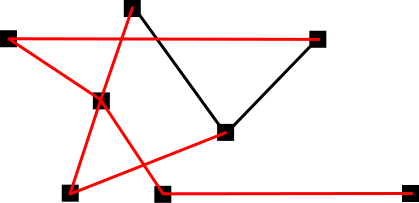
One thing to note is that every connected graph has a spanning tree.

A minimum weight spanning tree of an edge-weighted graph $G$ is a spanning tree of $G$ with the smallest possible sum of edge weights.

• previous
• next