Pigeonhole Principle, Inclusion-Exclusion

So, the pigeonhole principle. All that it says is this:

If there are more pigeons than pigeonholes, that means some holes must have more than $2$ pigeons.

It is a mapping rule: if there is a total injection from $A$ to $B$, then $|A| \leq |B|$.
That means, if $|A| \gt |B|$, there is no total injection.

If we have $n$ pigeons and $h$ holes, then some hole has more than or equal to $\lceil \frac{n}{h} \rceil$ (ceiling of $\frac{n}{h}$, ceiling being the rounded up value, e.g., $\lceil 2.0001 \rceil = 3$).

For example, let's say we have 7 pigeons and 6 pigeonholes. Dividing $7$ by $6$ is $1.16$, when we round up that value, we have $2$ as a result. So, one of the pigeonholes has $2$ pigeons in it.

Another example: ignoring leap years and assuming that one year has 365 days, the minimum number of people there has to be for at least 2 of them being born on the same day is 366.
Why is that? Well, imagine 365 people, there is a chance that each of them was born on different days. In order to make sure that at least 2 of them were born on the same day, there must be $k + 1$ people, making it 366.

Let's look at another example from the practice section of the course.

At a certain school, there are 11 different classes offered to first-year students, and each student must enroll in exactly 4 of them. How many students must be in one class year to guarantee that at least 2 students will have the same schedule?

This is firstly an n choose k problem, $n$ being 11, $k$ being 4. In order to have at least 2 students have the same schedule, we need to add 1 to the result.

So, what we need to do is this: $\frac{11!}{4! \cdot (11 - 4)!} + 1$.

We have 331 as the answer, so, there must be 331 students in one class year to guarantee that at least 2 students have the same schedule.

Let's take a look at the Principle of Inclusion-Exclusion.

We looked at the sum rule before, remember it says that if there are two disjoint sets, the size of their sum is the sum of the size of the first set and the size of the other set: $|A \cup B| = |A| + |B|$.

But, what if they are not disjoint? Like this:

Then, we would simply have to subtract the intersection from the above equation, and this is the principle of inclusion-exclusion:

The reason is that when we count $|A|$, we have already counted the intersection, and when we count $|B|$, that means we are doing it for the second time.

Another way to look at it is that when $A$ and $B$ are not disjoint, $A \cup B$ is the union of $A$ and all that is in $B$ that is not in $A$:

So, by the sum rule,

From the picture, it looks like $|B - A|$ is $|B| - |A \cap B|$. If that's true, we can prove the Principle of Inclusion-Exclusion. So in order to do that, let's prove this lemma which says $|B - A| = |B| - |A \cap B|$.

We can break the set $B$ into two pieces, two disjoint sets: the intersection part, and the rest:

Therefore, by the sum rule:

With a little arrangement, we see that

which was our starting point.

Plugging this definition of $|B - A|$ into $|A \cup B| = |A| + |B - A|$, we see:

Therefore, it proves our lemma, and the Principle of Inclusion-Exclusion. $\blacksquare$

What if we have three sets?
In that case, we would still subtract the intersections, but if we do, there will still be a small section where all the sets intersect that we need to add back in:

This picture taken from the slides of the lecture helps visualize it:

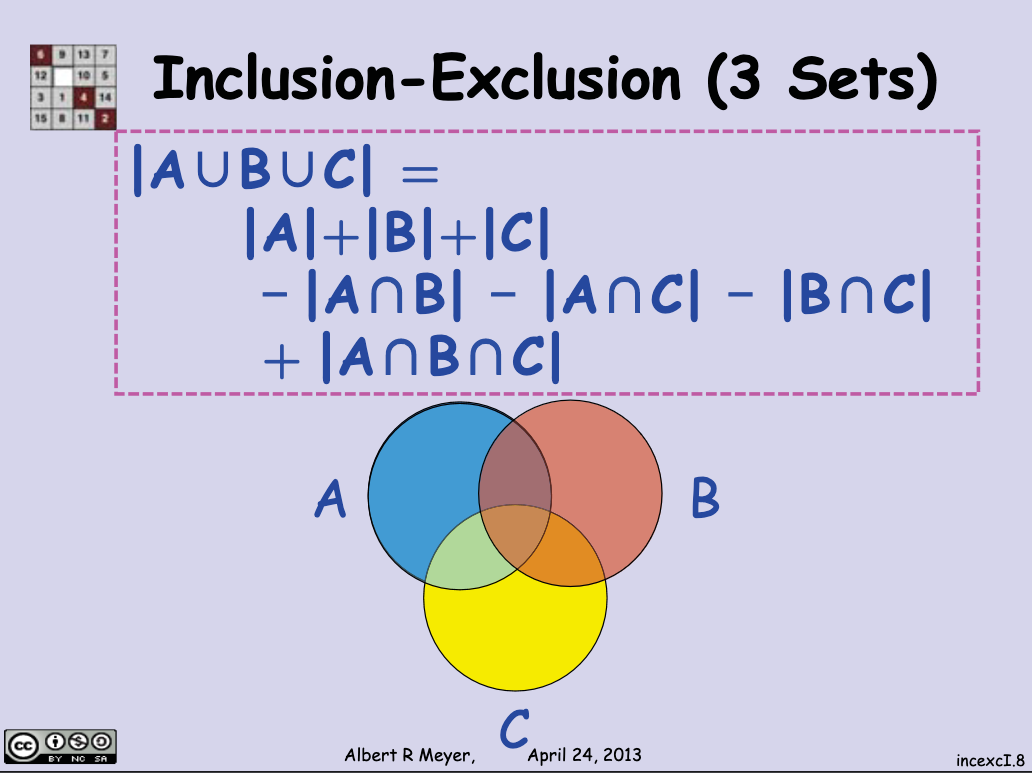
One thing to realize is that intersections with odd number of sets occur positively, and those with even numbers occur negatively. For example, $|A \cap B|$, or $|A \cap C|$, or, $|B \cap C|$ are intersections with $2$ sets, and they show up with a negative sign. But, $|A \cap B \cap C|$ has three sets, and it has a positive sign.

So, we have $n$ sets that are overlapping, and want to know the size of their union, $|A_1 \cup A_2 \cup \ ... \ \cup A_n|$.
We can express it as the sum of the sizes of the intersections, the sizes of the intersection $A_i$'s that are in this set of indices.
We need to specify the sign of that particular size of intersection, if it is odd, we want to add it with a positive sign; if it's even, we add it negatively. We can use $(-1)^{|S| + 1}$. If $|S|$ (the size of the intersection) is an odd number, it will be positive; if it's even, it'll be negative.

To write it down precisely:

• previous
• next