Sums & Products

Alright, let's start with arithmetic sums:

The sum of the first $n$ integers ($1 + 2 + ... + (n - 1) + n$) is:

Why?

Say that we are looking for the sum of numbers from 1 to 5. What we are looking for is the answer to $1 + 2 + 3 + 4 + 5$.

There is a constant amount of difference between each term, which is $1$. The difference between $2$ and $1$ is $1$, between $3$ and $2$ is $1$, and so on.
That means, we can write it as

Let's use $F$ to stand for our first term $1$, and $L$ to stand for our last term $5$. We can also use $d$ for the difference between terms, which is $1$.
$A$ is for the arithmetic sum, of course.

Then, we can write it as

Addition is commutative, we can reverse the order of the terms:

Let's add those two together, and see what we have, because why not:

$A = F + (F + d) + ... + (L - d) + L$
$A = L + (L - d) + ... + (F + d) + F$
$\underline{\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad +}$
$2A = (F + L) + (F + L) + ... + (F + L)$

If you didn't catch it, $d$'s are canceling out. And, what we have is

Dividing by $2$ to find $A$, we get what we have started with:

Substituting our first and last terms, clearly we have $\frac{1 + n}{2} \cdot n$. We can also write it as

With geometric sums, each sum is a multiple of the previous sum.

So, $G_n = 1 + x + x^2 + ... + x^n$.

The formula we have to find that is this:

Again, why?

Let's use another trick, different from the one we used for arithmetic sums.

This time let's multiply $G_n$ by $x$. This will increase the power of $x$ in each term:

Let's subtract it from the original $G_n$, because again, why not:

$G_n = 1 + x + x^2 + ... + x^n$
$-xG_n = -x -x^2 -x^3 - ... x^{n + 1}$
$\underline{\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad -}$
$G_n - xG_n = 1 - x^{n + 1}$

What we end up having is

We can factor $G_n$ out to have:

That means, $G_n$ is

We had simple formulas for arithmetic and geometric sums, but this time, we'll look at a formula that can give an estimation.

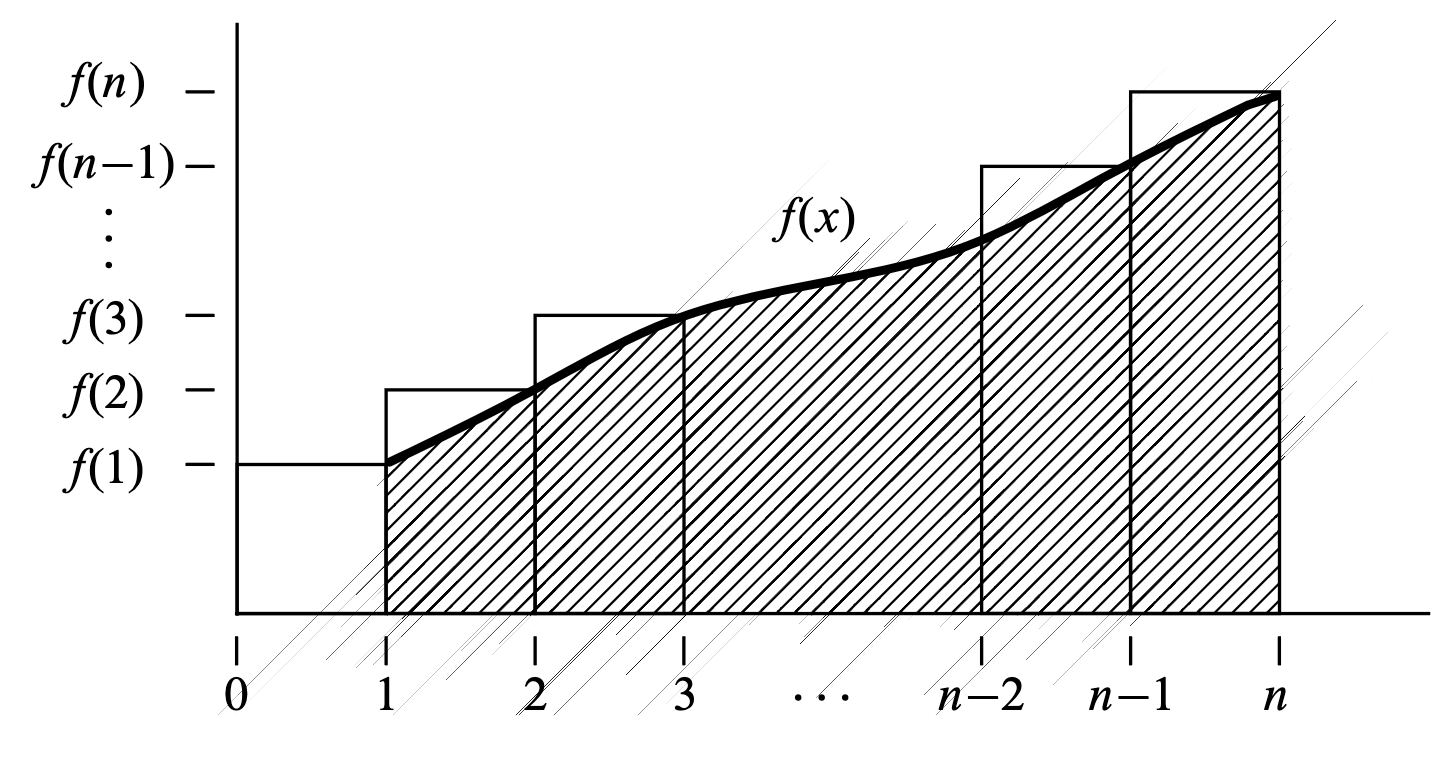
Let $f : \mathbb{R}^+ \rightarrow \mathbb{R}^+$ be a weakly increasing function.

The sum is:

Think of each term as a unit-width ($i$) rectangle, with a height of $f(i)$.
Then, the number for the sum we are looking for has to be the total area under the curve of $f(x)$.

The area under the curve $f(x)$ from $1$ to $n$ is:

Then:

Perhaps it would make more sense visually:

And, shift it left by $1$:

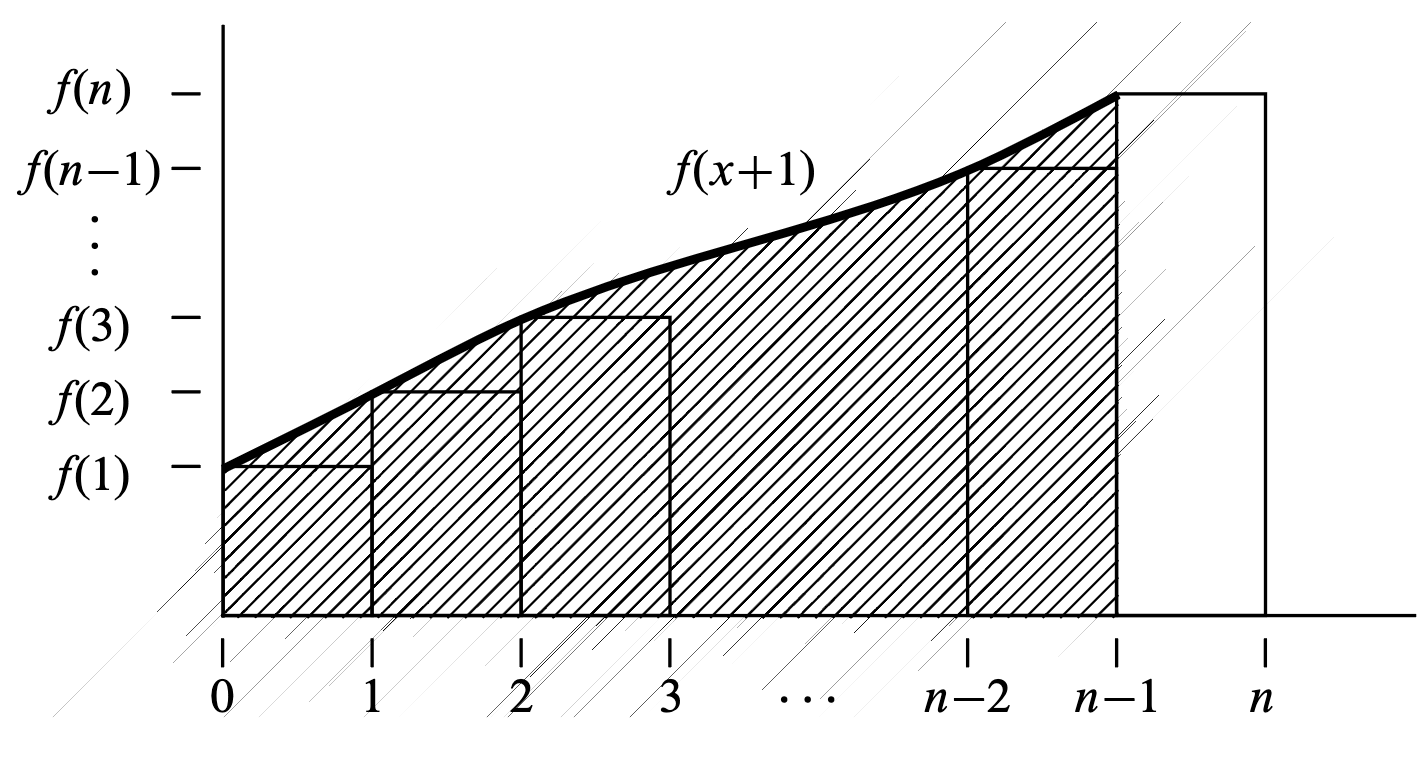
Figures 13.2 and 13.3 from the course notes Mathematics for Computer Science.

Any product can be converted into a sum by taking its logarithm.

Let's look at a factorial, for example, $n!$ is $1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot (n - 1) \cdot n$.

We can also denote it as:

It can be turned into a sum by taking the logarithm:

It is because of the product rule:

We have to estimate this sum to get a closed-form bound.
In order to do that, we are going to use the formula we defined above: $I + f(1) \leq S \leq I + f(n)$.

So, plugging them in:

Looks beautiful.

$ln(1)$ is $0$. So, it is just

After taking the integral, and exponentiating the whole thing (it was the product, remember, we are undoing it), the eventual result will be, according to the book:

One example of asymptotic equivalence is $(n^2 + n) \sim n^2$.

In order for two functions to be asymptotically equal, the limit of their quotient has to go to $1$ as $n$ approaches infinity. Let's see.

So, simplifying $\frac{n^2 + n}{n ^2}$ we have $1 + \frac{1}{n}$. As $n$ goes to $\infty$, $\frac{1}{n}$ goes to $0$, so we're left with $1$. And, that proves that $(n^2 + n)$ and $n^2$ are asymptotically equal.

• previous
• next