Intro to Discrete Probability

It doesn't matter how your relationship with probability theory was in the past, let's look at it with a fresh pair of eyes this time.

What we have in the first place is a set of random outcomes. Some portion of those outcomes (a subset) is an event. What we'll be looking for is the probability of an event:

Before looking at an example, we can keep in mind what is called a 4-part method:

1. Identify the outcomes
2. Identify the event
3. Assign outcome probabilities
4. Compute event probabilities

Now, let's look at an example from a practice exercise of the course.

Parker has two pairs of black shoes and three pairs of brown shoes. He also has three pairs of red socks, four pairs of brown socks and six pairs of black socks.
Now let's say that Parker chooses a pair of shoes at random and a pair of socks at random. We would like to know the probability of him choosing shoes and socks of the same color.

Let's construct a table to see what we have better:

The first thing we need to do is to identify the outcomes.
In this case, an outcome is a pair of colors.

The second thing to do is to identify the event of interest, to find $\frac{\text{number of outcomes in the event}}{\text{number of total outcomes}}$.

The number of total outcomes is $6$ (we have two possible colors for shoes—black and brown—, and three possible colors for socks: $2 \cdot 3 = 6$).

The number of outcomes in the event is $2$ because we can only have 2 colors that are in both shoes and socks: black and brown.

Now, the third step is to assign outcome probabilities. We have to do it for everything: So,

The final step is to compute the event probabilities to find the probability that he chooses shoes and socks of the same color.
In order to do that, let's look at the probability tree that is constructed:

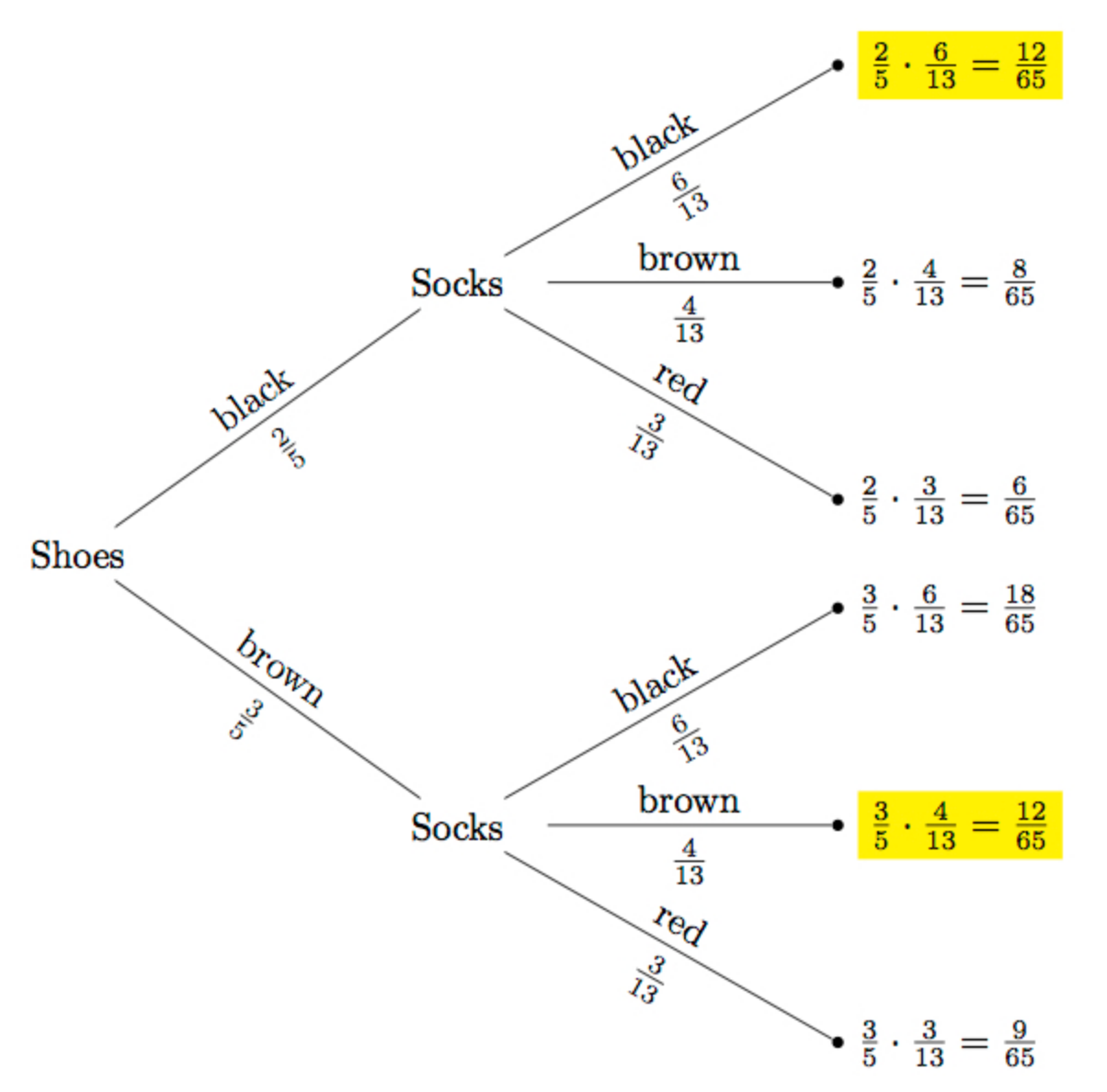
From Q4 Explanation.

Now that we see the probability of choosing black shoes and black socks is $\frac{12}{65}$ and the probability of choosing brown shoes and brown socks is $\frac{12}{65}$, we can sum the outcomes to find what we're looking for: $\frac{12}{65} + \frac{12}{65} = \frac{24}{65}$.
So, the probability of choosing the same color of shoes and socks is $\frac{24}{65} = 0.3692$.

Let's look at something called probability spaces.
A probability space consists of two things: a sample space and a probability function.

A sample space is a countable set $S$ whose elements are called outcomes.

A probability function is a function that assigns probabilities (ranging from $0$ to $1$ inclusive) to outcomes.
The sum of the probabilities of all the outcomes should add up to $1$.
Let $S$ be the sample space, and $\omega$ be an outcome in $S$.
So, we should have a probability function $Pr: S \rightarrow [0, \ 1]$ such that $\displaystyle\sum_{\omega \in S} \text{Pr}[\omega] = 1$.

The reason of constructing the tree model was to find a probability space.
So, the leaves of the tree correspond to outcomes; and we calculate the outcome probabilities from branch probabilities.

An event is a subset of the sample space, some set of outcomes.
The probability of an event is the sum of the probabilities of all the outcomes in the event:

From that, we get what is called the sum rule: if we have pairwise disjoint events $A_0, \ A_1, \ ...$ (meaning that there are no outcomes in common), the probability of one or more of these events occurring (their union) is the sum of each probability:

$\text{Pr}[A_0 \cup A_1 \cup A_2 \cup \ ...] = \text{Pr}[A_0] + \text{Pr}[A_0] + \text{Pr}[A_1] + \text{Pr}[A_2] + \ ...$

Defined precisely:

For example, if we have three pairwise disjoint events $E_0$, $E_1$, and $E_2$, each one with the probability of occurring $\frac{1}{4}$.
Then, the probability of any one of them occurring is $0.75$, because $\frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4} = 0.75$.

Now let's define some rules:

• previous
• next