LeetCode Meditations: Binary Tree Maximum Path Sum
![]()
Let's start with the description for Binary Tree Maximum Path Sum:
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node's values in the path.
Given the
rootof a binary tree, return the maximum path sum of any non-empty path.
For example:
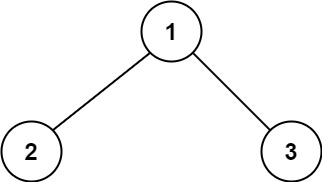
Input: root = [1, 2, 3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Input: root = [1, 2, 3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Or:
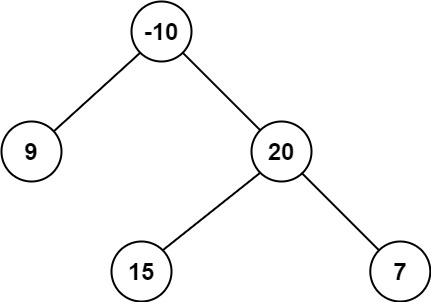
Input: root = [-10, 9, 20, null, null, 15, 7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Input: root = [-10, 9, 20, null, null, 15, 7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Although some people have found it quite simple, this is a challenging problem. So, we'll take a deep breath, and take a look at a recursive depth-first search approach as shown by NeetCode.
When all we have is a root node and its children, the maximum value we can have is the total values of all three of them. Of course, however, if there is a negative value that's going to lower the maximum value we can get, we shouldn't include it.
From any root node's perspective, what we should do is get the total maximum value from the left subtree and the total maximum value from the right subtree. However, if we do the same thing for a node in one of the subtrees, we'll break our path.
That is, if we are going to add the values of both of the children of a node, then we can't do that again for another node, because it will break the path. Once we have chosen both the left and right children of a node, we cannot have both children of another node again, we can only choose one of them. In other words, we can only split once.
Let's imagine that we are the root node. We'll get the values of both our left and right children. We'll get the maximum value we can get from our left subtree, but each node in the left subtree can choose only one of their children. The same is true for the right subtree as well:
/*
maxLeft: the maximum value gained from the left subtree
where each node chose only one of their children
maxRight: the maximum value gained from the right subtree
where each node chose only one of their children
*/
let currentMax = root.val + maxLeft + maxRight;
/*
maxLeft: the maximum value gained from the left subtree
where each node chose only one of their children
maxRight: the maximum value gained from the right subtree
where each node chose only one of their children
*/
let currentMax = root.val + maxLeft + maxRight;
Once again, the reason that the nodes in the subtrees have to choose only one of their children is that the root node have already chosen both of its children. Otherwise, our path will break.
But, how can we get maxLeft and maxRight?
That's where the depth-first of depth-first search comes in:
let maxLeft = dfs(root.left);
let maxRight = dfs(root.right);
let maxLeft = dfs(root.left);
let maxRight = dfs(root.right);
We'll initialize our result value as the minimum possible value of -Infinity (because we want to get the possible maximum):
let result = -Infinity;
let result = -Infinity;
Inside dfs, we need to update this value each time we calculate currentMax:
result = Math.max(result, currentMax);
result = Math.max(result, currentMax);
Remember that the nodes in the subtrees have to choose only one of their children? That's what our dfs function will return:
return Math.max(root.val + maxLeft, root.val + maxRight, 0);
return Math.max(root.val + maxLeft, root.val + maxRight, 0);
That's all there is to it. The final solution in TypeScript looks like this:
/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val === undefined ? 0 : val)
* this.left = (left === undefined ? null : left)
* this.right = (right === undefined ? null : right)
* }
* }
*/
function maxPathSum(root: TreeNode | null): number {
let result = -Infinity;
function dfs(root: TreeNode | null) {
if (root === null) {
return 0;
}
let maxLeft = dfs(root.left);
let maxRight = dfs(root.right);
let currentMax = root.val + maxLeft + maxRight;
result = Math.max(result, currentMax);
return Math.max(root.val + maxLeft, root.val + maxRight, 0);
}
dfs(root);
return result;
}
/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val === undefined ? 0 : val)
* this.left = (left === undefined ? null : left)
* this.right = (right === undefined ? null : right)
* }
* }
*/
function maxPathSum(root: TreeNode | null): number {
let result = -Infinity;
function dfs(root: TreeNode | null) {
if (root === null) {
return 0;
}
let maxLeft = dfs(root.left);
let maxRight = dfs(root.right);
let currentMax = root.val + maxLeft + maxRight;
result = Math.max(result, currentMax);
return Math.max(root.val + maxLeft, root.val + maxRight, 0);
}
dfs(root);
return result;
}
Time and space complexity
The time complexity is as we look at each node in the tree once. The space complexity is —where is the height of the tree—because of the stack frames created each time with the recursive calls.
It's time to take another deep breath, because next up is yet another problem that's labeled as hard — Serialize and Deserialize Binary Tree. Until then, happy coding.