LeetCode Meditations: Pacific Atlantic Water Flow
![]()
The description for this problem states:
There is an
m x nrectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.The island is partitioned into a grid of square cells. You are given an
m x ninteger matrixheightswhereheights[r][c]represents the height above sea level of the cell at coordinate(r, c).The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.
Return a 2D list of grid coordinates
resultwhereresult[i] = [ri, ci]denotes that rain water can flow from cell(ri, ci)to both the Pacific and Atlantic oceans.
For example:
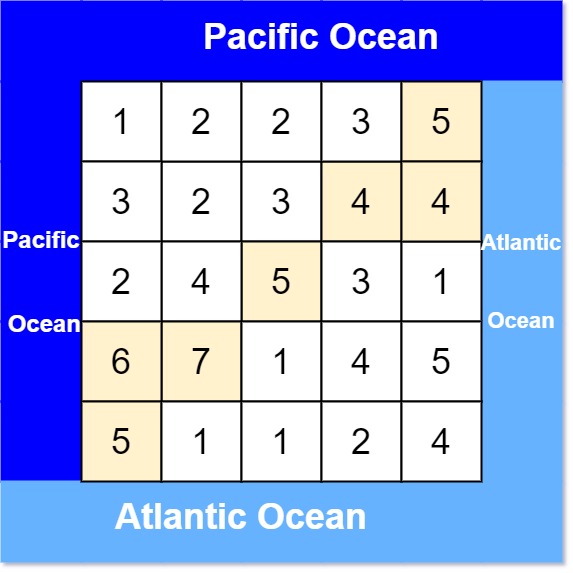
Input: heights = [
[1, 2, 2, 3, 5],
[3, 2, 3, 4, 4],
[2, 4, 5, 3, 1],
[6, 7, 1, 4, 5],
[5, 1, 1, 2, 4]
]
Output: [[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]]
Explanation: The following cells can flow to the Pacific and Atlantic oceans, as shown below:
[0, 4]: [0, 4] -> Pacific Ocean
[0, 4] -> Atlantic Ocean
[1, 3]: [1, 3] -> [0, 3] -> Pacific Ocean
[1, 3] -> [1, 4] -> Atlantic Ocean
[1, 4]: [1, 4] -> [1, 3] -> [0, 3] -> Pacific Ocean
[1, 4] -> Atlantic Ocean
[2, 2]: [2, 2] -> [1, 2] -> [0, 2] -> Pacific Ocean
[2, 2] -> [2, 3] -> [2, 4] -> Atlantic Ocean
[3, 0]: [3, 0] -> Pacific Ocean
[3, 0] -> [4, 0] -> Atlantic Ocean
[3, 1]: [3, 1] -> [3, 0] -> Pacific Ocean
[3, 1] -> [4, 1] -> Atlantic Ocean
[4, 0]: [4 ,0] -> Pacific Ocean
[4, 0] -> Atlantic Ocean
Note that there are other possible paths for these cells to flow to the Pacific and Atlantic oceans.
Input: heights = [
[1, 2, 2, 3, 5],
[3, 2, 3, 4, 4],
[2, 4, 5, 3, 1],
[6, 7, 1, 4, 5],
[5, 1, 1, 2, 4]
]
Output: [[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]]
Explanation: The following cells can flow to the Pacific and Atlantic oceans, as shown below:
[0, 4]: [0, 4] -> Pacific Ocean
[0, 4] -> Atlantic Ocean
[1, 3]: [1, 3] -> [0, 3] -> Pacific Ocean
[1, 3] -> [1, 4] -> Atlantic Ocean
[1, 4]: [1, 4] -> [1, 3] -> [0, 3] -> Pacific Ocean
[1, 4] -> Atlantic Ocean
[2, 2]: [2, 2] -> [1, 2] -> [0, 2] -> Pacific Ocean
[2, 2] -> [2, 3] -> [2, 4] -> Atlantic Ocean
[3, 0]: [3, 0] -> Pacific Ocean
[3, 0] -> [4, 0] -> Atlantic Ocean
[3, 1]: [3, 1] -> [3, 0] -> Pacific Ocean
[3, 1] -> [4, 1] -> Atlantic Ocean
[4, 0]: [4 ,0] -> Pacific Ocean
[4, 0] -> Atlantic Ocean
Note that there are other possible paths for these cells to flow to the Pacific and Atlantic oceans.
Although the description can be a challenge in itself to understand at first glance, what we need to do is essentially simple (at least, in theory). We want a cell whose neighbors are less than or equal to it, all the way to the north, south, east, and west until we reach both "oceans."
First, we can initialize two sets to store the cells that can reach "Pacific" and "Atlantic":
const reachableToPacific: Set<string> = new Set();
const reachableToAtlantic: Set<string> = new Set();
const reachableToPacific: Set<string> = new Set();
const reachableToAtlantic: Set<string> = new Set();
Instead of going cell by cell and checking if it can reach the oceans, we can first start by the cells that are adjacent to the oceans, and see which cells can reach us.
Since we're getting the cells that are reachable to oceans in different sets, we can return those that are in both sets (because we need to get those that are reachable to both oceans).
So, at the end, what we'll do is this:
for (const cell of reachableToPacific.values()) {
if (reachableToAtlantic.has(cell)) {
const [r, c] = cell.split(',');
result.push([+r, +c]);
}
}
for (const cell of reachableToPacific.values()) {
if (reachableToAtlantic.has(cell)) {
const [r, c] = cell.split(',');
result.push([+r, +c]);
}
}
We can use a breadth-first search to visit and mark the cells.
For the top and bottom edges of the grid, we'll mark the cells that can reach to Pacific and Atlantic:
for (let col = 0; col < colsLength; col++) {
bfs(0, col, reachableToPacific);
bfs(rowsLength - 1, col, reachableToAtlantic);
}
for (let col = 0; col < colsLength; col++) {
bfs(0, col, reachableToPacific);
bfs(rowsLength - 1, col, reachableToAtlantic);
}
We can do the similar thing for left and right edges of the grid as well:
for (let row = 0; row < rowsLength; row++) {
bfs(row, 0, reachableToPacific);
bfs(row, colsLength - 1, reachableToAtlantic);
}
for (let row = 0; row < rowsLength; row++) {
bfs(row, 0, reachableToPacific);
bfs(row, colsLength - 1, reachableToAtlantic);
}
Now, on to the implementation of bfs.
The purpose of our bfs function is to mark the cells that can reach to an "ocean." So, it'll take three parameters: r for row, c for column, and reachableToOcean for the set that stores the cells that are reachable.
As usual with BFS, we'll keep a queue that has arrays consisting of a row, a column, and the corresponding value in the grid:
let queue = [[r, c, heights[r][c]]];
let queue = [[r, c, heights[r][c]]];
As we go over the elements of queue, we'll mark a row-column pair as reachable as long as that pair is not out of bounds, or we haven't already added it as reachable, or the value it has is greater than or equal to the previous "height" we've looked at.
While queue is not empty, we'll first pop the current row, current column and previous height from queue:
const [currentRow, currentCol, prevHeight] = queue.pop() as number[];
const [currentRow, currentCol, prevHeight] = queue.pop() as number[];
If one of the conditions we mentioned above is true, we want to continue with the next element in the queue. Otherwise, we'll add it to our set:
if (
isOutOfBounds(currentRow, currentCol) ||
reachableToOcean.has(`${currentRow},${currentCol}`) ||
heights[currentRow][currentCol] < prevHeight
) {
continue;
}
reachableToOcean.add(`${currentRow},${currentCol}`);
if (
isOutOfBounds(currentRow, currentCol) ||
reachableToOcean.has(`${currentRow},${currentCol}`) ||
heights[currentRow][currentCol] < prevHeight
) {
continue;
}
reachableToOcean.add(`${currentRow},${currentCol}`);
Then, we'll add the neighbors to the queue, as well as heights[currentRow][currentCol], which is going to be the "previous height" for the next element:
// up, down, left, right
const coords = [[-1, 0], [1, 0], [0, -1], [0, 1]];
for (const [rowToGo, colToGo] of coords) {
queue.push([
currentRow + rowToGo,
currentCol + colToGo,
heights[currentRow][currentCol]
]);
}
// up, down, left, right
const coords = [[-1, 0], [1, 0], [0, -1], [0, 1]];
for (const [rowToGo, colToGo] of coords) {
queue.push([
currentRow + rowToGo,
currentCol + colToGo,
heights[currentRow][currentCol]
]);
}
And, that's it for the bfs function:
function bfs(r: number, c: number, reachableToOcean: Set<string>) {
let queue = [[r, c, heights[r][c]]];
while (queue.length > 0) {
const [currentRow, currentCol, prevHeight] = queue.pop() as number[];
if (
isOutOfBounds(currentRow, currentCol) ||
reachableToOcean.has(`${currentRow},${currentCol}`) ||
heights[currentRow][currentCol] < prevHeight
) {
continue;
}
reachableToOcean.add(`${currentRow},${currentCol}`);
// up, down, left, right
const coords = [[-1, 0], [1, 0], [0, -1], [0, 1]];
for (const [rowToGo, colToGo] of coords) {
queue.push([
currentRow + rowToGo,
currentCol + colToGo,
heights[currentRow][currentCol]
]);
}
}
}
function bfs(r: number, c: number, reachableToOcean: Set<string>) {
let queue = [[r, c, heights[r][c]]];
while (queue.length > 0) {
const [currentRow, currentCol, prevHeight] = queue.pop() as number[];
if (
isOutOfBounds(currentRow, currentCol) ||
reachableToOcean.has(`${currentRow},${currentCol}`) ||
heights[currentRow][currentCol] < prevHeight
) {
continue;
}
reachableToOcean.add(`${currentRow},${currentCol}`);
// up, down, left, right
const coords = [[-1, 0], [1, 0], [0, -1], [0, 1]];
for (const [rowToGo, colToGo] of coords) {
queue.push([
currentRow + rowToGo,
currentCol + colToGo,
heights[currentRow][currentCol]
]);
}
}
}
Putting everything together, here is what our final solution looks like in TypeScript:
function pacificAtlantic(heights: number[][]): number[][] {
let result = [];
const rowsLength = heights.length;
const colsLength = heights[0].length;
const reachableToPacific: Set<string> = new Set();
const reachableToAtlantic: Set<string> = new Set();
function isOutOfBounds(r: number, c: number) {
return r < 0 || c < 0 || r >= rowsLength || c >= colsLength;
}
function bfs(r: number, c: number, reachableToOcean: Set<string>) {
let queue = [[r, c, heights[r][c]]];
while (queue.length > 0) {
const [currentRow, currentCol, prevHeight] = queue.pop() as number[];
if (
isOutOfBounds(currentRow, currentCol) ||
reachableToOcean.has(`${currentRow},${currentCol}`) ||
heights[currentRow][currentCol] < prevHeight
) {
continue;
}
reachableToOcean.add(`${currentRow},${currentCol}`);
// up, down, left, right
const coords = [[-1, 0], [1, 0], [0, -1], [0, 1]];
for (const [rowToGo, colToGo] of coords) {
queue.push([
currentRow + rowToGo,
currentCol + colToGo,
heights[currentRow][currentCol]
]);
}
}
}
for (let col = 0; col < colsLength; col++) {
bfs(0, col, reachableToPacific);
bfs(rowsLength - 1, col, reachableToAtlantic);
}
for (let row = 0; row < rowsLength; row++) {
bfs(row, 0, reachableToPacific);
bfs(row, colsLength - 1, reachableToAtlantic);
}
for (const cell of reachableToPacific.values()) {
if (reachableToAtlantic.has(cell)) {
const [r, c] = cell.split(',');
result.push([+r, +c]);
}
}
return result;
}
function pacificAtlantic(heights: number[][]): number[][] {
let result = [];
const rowsLength = heights.length;
const colsLength = heights[0].length;
const reachableToPacific: Set<string> = new Set();
const reachableToAtlantic: Set<string> = new Set();
function isOutOfBounds(r: number, c: number) {
return r < 0 || c < 0 || r >= rowsLength || c >= colsLength;
}
function bfs(r: number, c: number, reachableToOcean: Set<string>) {
let queue = [[r, c, heights[r][c]]];
while (queue.length > 0) {
const [currentRow, currentCol, prevHeight] = queue.pop() as number[];
if (
isOutOfBounds(currentRow, currentCol) ||
reachableToOcean.has(`${currentRow},${currentCol}`) ||
heights[currentRow][currentCol] < prevHeight
) {
continue;
}
reachableToOcean.add(`${currentRow},${currentCol}`);
// up, down, left, right
const coords = [[-1, 0], [1, 0], [0, -1], [0, 1]];
for (const [rowToGo, colToGo] of coords) {
queue.push([
currentRow + rowToGo,
currentCol + colToGo,
heights[currentRow][currentCol]
]);
}
}
}
for (let col = 0; col < colsLength; col++) {
bfs(0, col, reachableToPacific);
bfs(rowsLength - 1, col, reachableToAtlantic);
}
for (let row = 0; row < rowsLength; row++) {
bfs(row, 0, reachableToPacific);
bfs(row, colsLength - 1, reachableToAtlantic);
}
for (const cell of reachableToPacific.values()) {
if (reachableToAtlantic.has(cell)) {
const [r, c] = cell.split(',');
result.push([+r, +c]);
}
}
return result;
}
Time and space complexity
The time complexity is — where is the number of rows, and is the number of columns, as we're traversing the whole grid but making use of the Set data structure to avoid visiting the same cell.
The space complexity is—I think—also , again, where is the number of rows, and is the number of columns. The size of our queue will grow proportionately to the size of the grid, and we also keep two sets, their sizes can also grow proportionately to the grid we're given.
The next and final problem we're going to look at in this chapter is Course Schedule. Until then, happy coding.