LeetCode Meditations: Word Search II
![]()
Let's start with the description for Word Search II:
Given an
m x nboardof characters and a list of stringswords, return all words on the board.Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
For example:
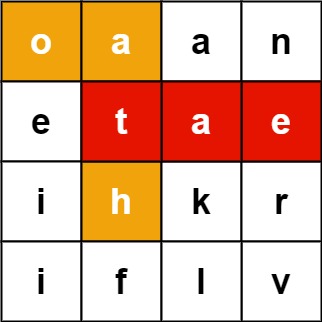
Input: board = [
['o', 'a', 'a', 'n'],
['e', 't', 'a', 'e'],
['i', 'h', 'k', 'r'],
['i', 'f', 'l', 'v'],
], words = ['oath', 'pea', 'eat', 'rain']
Output: ['eat', 'oath']
Input: board = [
['o', 'a', 'a', 'n'],
['e', 't', 'a', 'e'],
['i', 'h', 'k', 'r'],
['i', 'f', 'l', 'v'],
], words = ['oath', 'pea', 'eat', 'rain']
Output: ['eat', 'oath']
Or:
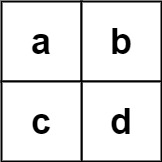
Input: board = [
['a', 'b'],
['c', 'd']
], words = ['abcb']
Output: []
Input: board = [
['a', 'b'],
['c', 'd']
], words = ['abcb']
Output: []
Also, our constraints are:
m == board.lengthn == board[i].length1 <= m, n <= 12board[i][j]is a lowercase English letter.1 <= words.length <= 3 * 10^41 <= words[i].length <= 10words[i]consists of lowercase English letters.- All the strings of
wordsare unique.
We've seen the first iteration of this problem where we needed to search for only one word. It's easy to think that, well, we can just loop over the words this time, and return those that our board has. Simple as that.
For example, if you remember the exist function (which uses depth-first search) that we implemented in the previous version of this problem, you might think that it's easy to do this:
function findWords(board: string[][], words: string[]): string[] {
let result = [];
for (const word of words) {
if (exist(board, word)) {
result.push(word);
}
}
return result;
}
function findWords(board: string[][], words: string[]): string[] {
let result = [];
for (const word of words) {
if (exist(board, word)) {
result.push(word);
}
}
return result;
}
However, this is going to be a terrible approach with a runtime of probably .
If we try that, we'll treat ourselves a good old Time Limit Exceeded error in one of the test cases. So, we need to find another way to solve this problem — which means it's time to take a deep breath.
Instead of going through each word in words and looking for it in board, we can look through board first. If the character we're looking at is in words, then we'll continue searching through its directions until we find the complete word (or not).
Because we're doing a character lookup (or basically, a prefix search), trie is going to be an efficient choice of data structure here.
Let's start with creating our simple trie node which has children, and a flag isEndOfWord to mark it as the end of the word character:
class TrieNode {
public children: Map<string, TrieNode>;
public isEndOfWord: boolean;
constructor() {
this.children = new Map();
this.isEndOfWord = false;
}
}
class TrieNode {
public children: Map<string, TrieNode>;
public isEndOfWord: boolean;
constructor() {
this.children = new Map();
this.isEndOfWord = false;
}
}
Then, we'll create our trie, but for now, we'll only have an addWord method. This is exactly what we've seen for the last two problems, so it's easy:
class Trie {
public root: TrieNode;
constructor() {
this.root = new TrieNode();
}
addWord(word: string) {
let currentNode = this.root;
for (const char of word) {
if (!currentNode.children.has(char)) {
currentNode.children.set(char, new TrieNode());
}
currentNode = currentNode.children.get(char) as TrieNode;
}
currentNode.isEndOfWord = true;
}
}
class Trie {
public root: TrieNode;
constructor() {
this.root = new TrieNode();
}
addWord(word: string) {
let currentNode = this.root;
for (const char of word) {
if (!currentNode.children.has(char)) {
currentNode.children.set(char, new TrieNode());
}
currentNode = currentNode.children.get(char) as TrieNode;
}
currentNode.isEndOfWord = true;
}
}
Traversing each character in word, we add it to our trie, updating the current node (which starts as our root node, of course) as we go. Once we reach the last character, we mark it as the end of the word.
Now, the first thing to do if we want to look up the words in our trie is... to add them to our trie, of course!
Inside the findWords function, we can do that easily:
let trie = new Trie();
for (const word of words) {
trie.addWord(word);
}
let trie = new Trie();
for (const word of words) {
trie.addWord(word);
}
We'll also have a result array to add the words that are in board:
let result: string[] = [];
let result: string[] = [];
This array will be modified by the function that does the depth-first search, so that at the end of our main function findWords, we can just return it.
For each cell, we'll run a depth-first search if that character is the start of a word in words:
for (let i = 0; i < rowsLength; i++) {
for (let j = 0; j < colsLength; j++) {
if (trie.root.children.has(board[i][j])) {
dfs(i, j, trie.root.children.get(board[i][j]) as TrieNode, []);
}
}
}
for (let i = 0; i < rowsLength; i++) {
for (let j = 0; j < colsLength; j++) {
if (trie.root.children.has(board[i][j])) {
dfs(i, j, trie.root.children.get(board[i][j]) as TrieNode, []);
}
}
}
So, if board[i][j] (which is the current character) is the first character of a word in words, we'll run dfs, passing it the arguments of the current row and column, as well as the next character (trie.root.children.get(board[i][j])). We'll also pass it an empty array to keep track of the path we're exploring.
Now let's look at the dfs function itself.
The first thing we need to do is to add the current character (the current cell) to our path, and mark it as "visited." We can mark it with an asterisk (*) to do that:
let currentChar = board[currentRow][currentCol];
path.push(currentChar);
board[currentRow][currentCol] = '*';
let currentChar = board[currentRow][currentCol];
path.push(currentChar);
board[currentRow][currentCol] = '*';
Now, if the current node we're looking at is the end character of a word, that means our path consists of all the letters of a word in words, so we can add it to result as a string. After that, we'll mark that node as not the end of a word, because in our next iterations, that node might not be the end character of another word:
if (currentNode.isEndOfWord) {
result.push(path.join(''));
currentNode.isEndOfWord = false;
}
if (currentNode.isEndOfWord) {
result.push(path.join(''));
currentNode.isEndOfWord = false;
}
From that current cell, we'll look at all the directions we can go as long as we stay within the bounds of board, and that next character is the next character in that word (if it's a child node of the current node):
// Coordinations to go right, left, down, and up
let coords = [[0, 1], [0, -1], [1, 0], [-1, 0]];
for (const [r, c] of coords) {
let [rowToGo, colToGo] = [currentRow + r, currentCol + c];
if (!outOfBounds(rowToGo, colToGo) && currentNode.children.has(board[rowToGo][colToGo])) {
dfs(
rowToGo,
colToGo,
currentNode.children.get(board[rowToGo][colToGo]) as TrieNode,
path
);
}
}
// Coordinations to go right, left, down, and up
let coords = [[0, 1], [0, -1], [1, 0], [-1, 0]];
for (const [r, c] of coords) {
let [rowToGo, colToGo] = [currentRow + r, currentCol + c];
if (!outOfBounds(rowToGo, colToGo) && currentNode.children.has(board[rowToGo][colToGo])) {
dfs(
rowToGo,
colToGo,
currentNode.children.get(board[rowToGo][colToGo]) as TrieNode,
path
);
}
}
Once we have done exploring our options, we need to backtrack, so we need to pop the last character from our path and reset the cell to its original character:
path.pop();
board[currentRow][currentCol] = currentChar;
path.pop();
board[currentRow][currentCol] = currentChar;
And, that's pretty much it for the dfs function:
function dfs(currentRow: number, currentCol: number, currentNode: TrieNode, path: string[]) {
let currentChar = board[currentRow][currentCol];
path.push(currentChar);
board[currentRow][currentCol] = '*';
// If we find a word, we'll add it to result, and
// mark that node as not the end character
// because it might be in another word
if (currentNode.isEndOfWord) {
result.push(path.join(''));
currentNode.isEndOfWord = false;
}
// Coordinations to go right, left, down, and up
let coords = [[0, 1], [0, -1], [1, 0], [-1, 0]];
for (const [r, c] of coords) {
let [rowToGo, colToGo] = [currentRow + r, currentCol + c];
if (!outOfBounds(rowToGo, colToGo) && currentNode.children.has(board[rowToGo][colToGo])) {
dfs(
rowToGo,
colToGo,
currentNode.children.get(board[rowToGo][colToGo]) as TrieNode,
path
);
}
}
path.pop();
board[currentRow][currentCol] = currentChar;
}
function dfs(currentRow: number, currentCol: number, currentNode: TrieNode, path: string[]) {
let currentChar = board[currentRow][currentCol];
path.push(currentChar);
board[currentRow][currentCol] = '*';
// If we find a word, we'll add it to result, and
// mark that node as not the end character
// because it might be in another word
if (currentNode.isEndOfWord) {
result.push(path.join(''));
currentNode.isEndOfWord = false;
}
// Coordinations to go right, left, down, and up
let coords = [[0, 1], [0, -1], [1, 0], [-1, 0]];
for (const [r, c] of coords) {
let [rowToGo, colToGo] = [currentRow + r, currentCol + c];
if (!outOfBounds(rowToGo, colToGo) && currentNode.children.has(board[rowToGo][colToGo])) {
dfs(
rowToGo,
colToGo,
currentNode.children.get(board[rowToGo][colToGo]) as TrieNode,
path
);
}
}
path.pop();
board[currentRow][currentCol] = currentChar;
}
And, the whole solution looks like this:
class TrieNode {
public children: Map<string, TrieNode>;
public isEndOfWord: boolean;
constructor() {
this.children = new Map();
this.isEndOfWord = false;
}
}
class Trie {
public root: TrieNode;
constructor() {
this.root = new TrieNode();
}
addWord(word: string) {
let currentNode = this.root;
for (const char of word) {
if (!currentNode.children.has(char)) {
currentNode.children.set(char, new TrieNode());
}
currentNode = currentNode.children.get(char) as TrieNode;
}
currentNode.isEndOfWord = true;
}
}
function findWords(board: string[][], words: string[]): string[] {
const rowsLength = board.length;
const colsLength = board[0].length;
function outOfBounds(r: number, c: number) {
return r < 0 || c < 0 || r >= rowsLength || c >= colsLength;
}
let result: string[] = [];
let trie = new Trie();
for (const word of words) {
trie.addWord(word);
}
function dfs(currentRow: number, currentCol: number, currentNode: TrieNode, path: string[]) {
let currentChar = board[currentRow][currentCol];
path.push(currentChar);
board[currentRow][currentCol] = '*';
// If we find a word, we'll add it to result, and
// mark that node as not the end character
// because it might be in another word
if (currentNode.isEndOfWord) {
result.push(path.join(''));
currentNode.isEndOfWord = false;
}
// Coordinations to go right, left, down, and up
let coords = [[0, 1], [0, -1], [1, 0], [-1, 0]];
for (const [r, c] of coords) {
let [rowToGo, colToGo] = [currentRow + r, currentCol + c];
if (!outOfBounds(rowToGo, colToGo) && currentNode.children.has(board[rowToGo][colToGo])) {
dfs(
rowToGo,
colToGo,
currentNode.children.get(board[rowToGo][colToGo]) as TrieNode,
path
);
}
}
path.pop();
board[currentRow][currentCol] = currentChar;
}
for (let i = 0; i < rowsLength; i++) {
for (let j = 0; j < colsLength; j++) {
if (trie.root.children.has(board[i][j])) {
dfs(i, j, trie.root.children.get(board[i][j]) as TrieNode, []);
}
}
}
return result;
}
class TrieNode {
public children: Map<string, TrieNode>;
public isEndOfWord: boolean;
constructor() {
this.children = new Map();
this.isEndOfWord = false;
}
}
class Trie {
public root: TrieNode;
constructor() {
this.root = new TrieNode();
}
addWord(word: string) {
let currentNode = this.root;
for (const char of word) {
if (!currentNode.children.has(char)) {
currentNode.children.set(char, new TrieNode());
}
currentNode = currentNode.children.get(char) as TrieNode;
}
currentNode.isEndOfWord = true;
}
}
function findWords(board: string[][], words: string[]): string[] {
const rowsLength = board.length;
const colsLength = board[0].length;
function outOfBounds(r: number, c: number) {
return r < 0 || c < 0 || r >= rowsLength || c >= colsLength;
}
let result: string[] = [];
let trie = new Trie();
for (const word of words) {
trie.addWord(word);
}
function dfs(currentRow: number, currentCol: number, currentNode: TrieNode, path: string[]) {
let currentChar = board[currentRow][currentCol];
path.push(currentChar);
board[currentRow][currentCol] = '*';
// If we find a word, we'll add it to result, and
// mark that node as not the end character
// because it might be in another word
if (currentNode.isEndOfWord) {
result.push(path.join(''));
currentNode.isEndOfWord = false;
}
// Coordinations to go right, left, down, and up
let coords = [[0, 1], [0, -1], [1, 0], [-1, 0]];
for (const [r, c] of coords) {
let [rowToGo, colToGo] = [currentRow + r, currentCol + c];
if (!outOfBounds(rowToGo, colToGo) && currentNode.children.has(board[rowToGo][colToGo])) {
dfs(
rowToGo,
colToGo,
currentNode.children.get(board[rowToGo][colToGo]) as TrieNode,
path
);
}
}
path.pop();
board[currentRow][currentCol] = currentChar;
}
for (let i = 0; i < rowsLength; i++) {
for (let j = 0; j < colsLength; j++) {
if (trie.root.children.has(board[i][j])) {
dfs(i, j, trie.root.children.get(board[i][j]) as TrieNode, []);
}
}
}
return result;
}
Time and space complexity
The time complexity of findWords can be, in the worst case, where is the length of rows, is the length of columns, and is the total number of words — because we might explore all the cells searching for each word.
For the space complexity, first, we have our trie whose storage needs will grow as the total number of characters in words grow. We can say that it's where is the number of all characters in words. We also store a path array in our depth-first search, in the worst case where we need to store every unique cell, we'll end up storing the whole board, so it can have space complexity where is the length of rows and is the length of columns.
Combining them together, I think, the space complexity might end up being .
If some of the parts still doesn't make sense, that's okay. This is a very, very tough problem, and honestly, backtracking is one of the most challenging concepts that's somewhat easy to wrap your mind around theoretically, but not so easy in practice.
Now that we're done with this chapter as well, it's time for another deep breath. Next up, we'll take a look at the graph data structure. Until then, happy coding.